Penemuan Integral (Konsep Integral)
A. Tokoh Penemu Integral
1.
Archimedes

Archimedes dari Syracusa (sekitar 287 SM -
212 SM). Ia adalah fisikawan dan matematikawn
penemu dari Yunani yang terkenal. Ia belajar di kota
Alexandria, Mesir. Pada waktu itu yang menjadi raja di Sirakusa adalah Hieron
II, sahabat Archimedes. Archimedes sendiri adalah seorang matematikawan, astronom, filsuf, fisikawan, dan insinyur berbangsa Yunani.
Archimedes menggunakan ide integral tersebut untuk mencari luas daerah suatu
lingkaran, luas daerah yang dibatasi oleh parabola dan tali busur, dan
sebagainya.
2. Gottfried Wilhem
Leibniz

Gottfried Wilhem
Leibniz atau
kadangkala dieja sebagai Leibnitz
atau Von Leibniz (1 Juli
(21 Juni menurut tarikh kalender Julian) 1646 – 14 November 1716) adalah seorang filsuf Jerman keturunan Sorbia dan berasal dari Sachsen. Selain seorang filsuf,
ia adalah ilmuwan, matematikawan, diplomat, fisikawan, sejarawan dan doktor dalam hukum duniawi dan hukum
gereja.
Leibniz
dipercaya bersama dengan Sir Isaac Newton, dengan penemuan kalkulus
(diferensial dan kalkulus integral). Menurut notebook Leibniz, terobosan
penting terjadi pada 11 November, 1675, ketika ia bekerja kalkulus integral
untuk pertama kalinya menemukan area di bawah grafik fungsi
.
Dia
memperkenalkan beberapa notasi yang digunakan sampai hari ini, misalnya tanda
integral, mewakali S memanjang, dari kata
Latin
summa, dan
digunakan untuk selisih, dari kata diferensial
Latin. Ini notasi cerdik sugestif untuk kalkulus mungkin warisan matematika
paling abadi. Leibniz tidak mempublikasikan apa-apa tentang kalkulus sampai
1684. Leibniz menyatakan hubungan terbalik integrasi dan diferensial, kemudian
disebut teorema dasar kalkulus, dengan cara maksud bentuknya tahun 1693 dalam
karangan Supplementum geometriae
dimensoriae. Namun, James Gregory dipercaya untuk penemuan teorema dalam
bentuk geometris, Isaac Barrow membuktikan versi geometris yang lebih umum, dan
Newton mengembangkan teori pendukung. Konsep menjadi lebih transparan
dikembangkan melalui formalisme Leibniz dan notasi baru. Aturan produk kalkulus
diferensial masih disebut "hukum Leibniz". Selain itu, teorema yang
memberitahu bagaimana dan kapan untuk membedakan dalam tanda integral disebut
Leibniz aturan terpisahkan.
3. Issac Newton

Kebanyakan ahli sejarah percaya bahwa Newton dan Leibniz mengembangkan kalkulus secara terpisah. Keduanya pula menggunakan notasi matematika yang
berbeda pula. Menurut teman-teman dekat Newton, Newton telah menyelesaikan
karyanya bertahun-tahun sebelum Leibniz, namun tidak mempublikasikannya sampai
dengan tahun 1693. Ia pula baru menjelaskannya secara penuh pada tahun 1704,
manakala pada tahun 1684, Leibniz sudah mulai mempublikasikan penjelasan penuh
atas karyanya. Notasi dan "metode diferensial" Leibniz secara universal
diadopsi di Daratan Eropa, sedangkan Kerajaan Britania baru mengadopsinya setelah tahun 1820.
4. Georg Friedrich Bernhard
Riemann

Georg
Friedrich Bernhard Riemann (lahir 17 September 1826 – meninggal 20 Juli 1866 pada umur 39 tahun) (diucapkan REE mahn) ialah matematikawan Jerman yang membuat sumbangan
penting pada analisis dan geometri diferensial, beberapa darinya meratakan
jalan untuk pengembangan lebih lanjut pada relativitas umum. Namanya dihubungkan dengan fungsi zeta Riemann, integral Riemann, lema
Riemann, manipol
Riemann, teorema pemetaan Riemann, problem Riemann-Hilbert, teorema
Riemann-Roch, persamaan Cauchy-Riemann dll.
Integral
Riemann, dalam cabang matematika yang dikenal sebagai analisis riil, merupakan definisi ketat
pertama integral sebuah fungsi dalam sebuah selang. Meskipun integral Riemann
tidak cocok untuk banyak kegunaan teoretis, integral ini merupakan salah satu
integral yang paling mudah untuk didefinisikan. Sebagian kekurangan teknis ini
dapat diperbaiki oleh integral Riemann-Stieltjes, dan kebanyakan tidak ada
lagi pada integral Lebesgue.
B. Konsep Dasar Integral
Integral adalah sebuah konsep penjumlahan secara berkesinambungan dalam matematika, dan bersama dengan inversnya. Diferensiasi adalah satu dari dua operasi utama dalam kalkulus. Integral dikembangkan menyusul dikembangkannya masalah dalam diferensiasi di mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi.
Integral adalah sebuah konsep penjumlahan secara berkesinambungan dalam matematika, dan bersama dengan inversnya. Diferensiasi adalah satu dari dua operasi utama dalam kalkulus. Integral dikembangkan menyusul dikembangkannya masalah dalam diferensiasi di mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi.
1. Integral Tak Tentu
Misalkan fungsi f adalah turunan dari fungsi F, yang berarti
Pandanglah pendiferensialan fungsi-fungsi di bawah ini
Sekarang timbul pertanyaan apakah dari hubungan F'(x) = f(x) ini jika f(x) diketahui maka f(x) pasti dapat ditentukan ?
Suatu operasi mencari F(x) jika f(x) diketahui yang merupakan invers dari operasi pendiferensialan disebut operasi anti derivatif, anti diferensial, anti turunan yang biasa disebut Operasi integral. Dari contoh di atas dapat ditarik kesimpulan bahwa anti turunan dari
Dari pengertian bahwa integral adalah invers dari Operasi pendiferensialan, maka apabila terdapat fungsi F(x) yang diferensial pada interval [a, b] sedemikian hingga
dengan c sembarangan konstanta.
Dari contoh diatas diperoleh hasil  . Dengan memerhatikan diferensial-diferensial dibawah ini:
. Dengan memerhatikan diferensial-diferensial dibawah ini:
maka diperoleh integral fungsi-fungsi aljabar :
Jika f(x) dan g(x) merupakan dua fungsi yang dapat di integralkan dan c, k bilangan real, maka:
Contoh :
1. Tentukan
Jawab:
2. Tentukan
Jawab:
Mengingat pendiferensialan fungsi-fungsi yang lain, yaitu:
Jika
Jika
Jika
Jika
Jika
Jika
Jika
Jika
Adapun rumus dasar integral trigonometri dapat dirumuskan sebagai berikut.
Berkaitan dengan penyelesaian integral fungsi trigonometri, biasanya memerlukan hubungan perbandingan trigonometri berikut.
Contoh :
1. Tentukan
Jawab :
2. Tentukan
Jawab:
2 . Integral Tertentu

Gambar diatas memperlihatkan daerah L yang dibatasi oleh y = f(x), sumbu x dari x = a sampai dengan x = b. Untuk mencari luas daerah L ditempuh langkah- langkah sebagai berikut.
Langkah pertama, interval [a,b] dibagi menjadi n interval dengan panjang masing- masing interval bagian Δx1, Δx2, Δx3, …, Δxn. Sedang pada masing-masing interval ditentukan titik-titik x1, x2, x3, …, xn. Selanjutnya dibuat persegipanjang-persegi- panjang dengan panjang masing-masing f(x1), f(x2), f(x3), …, f(xn) dan lebar masing- masing Δx1, Δx2, Δx3, …, Δxn sehingga :
Luas persegi panjang pertama = f(x1) . Δx1
Luas persegi panjang kedua = f(x2) . Δx2
Luas persegi panjang ketiga = f(x3) . Δx3
Luas persegi panjang ke- n = f(xn) . Δxn
Jumlah luas seluruh persegi panjang = f(x1) . Δx1 + f(x2) . Δx2 + f(x3) . Δx3 +...+ f(xn) . Δxn
=&space;\&space;.&space;\Delta&space;x_{i})
Dan untuk menekankan bahwa pengambilan jumlah tersebut meliputi daerah pada interval [a,b], notasi sigma di atas sering kita tulis dengan notasi.
Jumlah luas persegi panjang =
\&space;.\&space;\Delta&space;x)
Jika n dibuat cukup besar maka jumlah luas diatas mendekati luas daerah L. Sehingga luas daeah L adalah nilai limit jumlah di atas.
&space;\&space;.&space;\&space;\Delta&space;x)
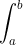 : notasi integral tertentu
: notasi integral tertentu
a : batas bawah integral
b : batas atas integral
Misalkan fkontinu pada interval tertutup [a,b] atau a ≤ x ≤ b. Jika F suatu fungsi sedemikian rupa sehiingga F^' (x)=f(x) untuk semua x pada [a,b] maka berlaku
![\int_{a}^{b} f(x) \ dx \ =\left [ F(x) \right ]_a^b = F(b) - F(a)](https://latex.codecogs.com/gif.latex?\int_{a}^{b}&space;f(x)&space;\&space;dx&space;\&space;=\left&space;[&space;F(x)&space;\right&space;]_a^b&space;=&space;F(b)&space;-&space;F(a))
F(x) adalah antiturunan dari f(x) pada a ≤ x ≤ b. Hubungan di atas dinamakan dengan teorema dasar kalkulus. Dengan teorema ini, nilai integral tertentu lebih mudah diketahui.
Notasi tersebut di atas biasa ditulis dengan notasi integral tertentu atau integral Riemann: &space;\&space;dx)
Keterangan :a : batas bawah integral
b : batas atas integral
Misalkan fkontinu pada interval tertutup [a,b] atau a ≤ x ≤ b. Jika F suatu fungsi sedemikian rupa sehiingga F^' (x)=f(x) untuk semua x pada [a,b] maka berlaku
F(x) adalah antiturunan dari f(x) pada a ≤ x ≤ b. Hubungan di atas dinamakan dengan teorema dasar kalkulus. Dengan teorema ini, nilai integral tertentu lebih mudah diketahui.
Contoh :
1. Tentukan nilai integral dari &space;dx)
Jawab:
![\int_{1}^{3} (2x+3) dx= [x^2+3x]_{1}^{3}](https://latex.codecogs.com/gif.latex?\int_{1}^{3}&space;(2x+3)&space;dx=&space;[x^2+3x]_{1}^{3})
&space;\&space;-&space;\&space;(1^2+3\&space;.&space;\1&space;))
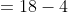

2. Tentukan nilai dari&space;dx)
Jawab:
![\int_{1}^{5} (x-3) dx=[\frac{1}{2}x^2-3x]_{1}^{5}](https://latex.codecogs.com/gif.latex?\int_{1}^{5}&space;(x-3)&space;dx=[\frac{1}{2}x^2-3x]_{1}^{5})
-(\frac{1}{2}1^2-3&space;\&space;.&space;\&space;1))
-(\frac{1}{2}1^2-3&space;\&space;.&space;\&space;1))
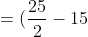-(\frac{1}{2}-3))
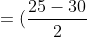-(\frac{1-6}{2}))
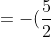+(\frac{5}{2}))
Jawab:
2. Tentukan nilai dari
Jawab:



jadi tahu tokoh2 penemunya
ReplyDeleteElever Agency