Sejarah Phytagoras
Pythagoras adalah seorang matematikawan
dan filsuf Yunani yang paling dikenal melalui teoremanya.Dikenal
sebagai "Bapak Bilangan", dia memberikan sumbangan yang penting
terhadap filsafat dan ajaran keagamaan pada akhir abad ke-6 SM. Phytagoras
memiliki peran yang besar terhadap dunia Matematika. Salah satu peninggalan
Pythagoras yang terkenal adalah teorema Pythagoras, yang menyatakan bahwa
kuadrat hipotenusa dari suatu segitiga siku-siku adalah sama
dengan jumlah kuadrat dari kaki-kakinya (sisi-sisi siku-sikunya). Walaupun
fakta di dalam teorema ini telah banyak diketahui sebelum lahirnya
Pythagoras, namun teorema ini dikreditkan kepada Pythagoras karena ia yang
pertama kali membuktikan pengamatan ini secara matematis.
Pythagoras
dan murid-muridnya percaya bahwa segala sesuatu di dunia ini berhubungan dengan
matematika, dan merasa bahwa segalanya dapat diprediksikan dan diukur
dalam siklus beritme. Ia percaya keindahan matematika disebabkan
segala fenomena alam dapat dinyatakan dalam bilangan-bilangan
atau perbandingan bilangan. Selain teorema Phytagoras masih ada beberapa
aliran matematika Phytagoras yang mempengaruhi perkembangan matematika dunia
saat ini yang perlu kita ketahui.
Sejarah Teorema Phytagoras
Pythagoras
(569-500 SM) lahir di Pulau Samos di Yunani, dan melakukan banyak perjalanan
melalui Mesir, belajar, antara lain, matematika. Tidak banyak yang
diketahui dari Phytagoras pada tahun-tahun awal. Pythagoras menjadi
terkenal setelah mendirikan sebuah kelompok, “the Brotherhood of
Pythagoreans” (Persaudaraan ilmu Pythagoras), yang dikhususkan untuk
mempelajari matematika. Kelompok ini sangat dikultuskan sebagai simbol,
ritual dan doa. Selain itu, Pythagoras percaya bahwa “Banyak aturan alam
semesta,” dan ilmu Pythagoras memberikan nilai numerik untuk banyak obyek dan
gagasan. Nilai-nilai numerik, pada gilirannya, dihubungkan dengan nilai
mistik dan spiritual.
Legenda
mengatakan bahwa setelah menyelesaiakan teorema yang terkenal itu, Pythagoras
mengorbankan 100 lembu. Meskipun ia sangat diagungkan dengan penemuan
teorema yang terkenal itu, namun tidaklah jelas diketahui apakah Pythagoras
adalah penulis yang sebenarnya. Para pengkaji dalam kelompok the
Brotherhood of Pythagoreans telah menulis banyak bukti geometris, tetapi
sulit untuk dipastikan siapa penemu Teorema Phytagoras itu sendiri, sungguh
sebuah kelompok yang sangat menjaga rahasia temuan mereka. Sayangnya,
sumpah kerahasiaan tersebut bertentangan dengan ide matematika yang penting
yang harus diketahui publik. Kelompok the Brotherhood of Pythagoreans
telah menemukan bilangan irasional! Jika kita mengambil segitiga siku-siku
sama kaki dengan kaki ukuran 1, maka panjang sisi miring adalah  . Namun
jumlah ini tidak dapat dinyatakan sebagai panjang yang dapat diukur dengan
penggaris dibagi menjadi beberapa bagian pecahan, dan ini sangat mengganggu
Kelompok Pythagoras, yang terlanjur percaya bahwa “Semua adalah
angka.” Mereka menyebutnya angka-angka “alogon,” yang berarti “unutterable.” Akhirnya
mereka sangat terkejut dengan angka-angka ini, sehingga mereka dihukum mati
seorang anggota yang berani menyebutkan keberadaan mereka kepada
publik. Barulah 200 tahun kemudian, yaitu oleh Eudoxus, seorang
matematikawan Yunani yang dapat mengembangkan sebuah cara untuk berurusan
dengan angka-angka unutterable tersebut.
. Namun
jumlah ini tidak dapat dinyatakan sebagai panjang yang dapat diukur dengan
penggaris dibagi menjadi beberapa bagian pecahan, dan ini sangat mengganggu
Kelompok Pythagoras, yang terlanjur percaya bahwa “Semua adalah
angka.” Mereka menyebutnya angka-angka “alogon,” yang berarti “unutterable.” Akhirnya
mereka sangat terkejut dengan angka-angka ini, sehingga mereka dihukum mati
seorang anggota yang berani menyebutkan keberadaan mereka kepada
publik. Barulah 200 tahun kemudian, yaitu oleh Eudoxus, seorang
matematikawan Yunani yang dapat mengembangkan sebuah cara untuk berurusan
dengan angka-angka unutterable tersebut.
Setelah ditemukan oleh Kelompok
Pythagoras, namun menolak untuk mengakui keberadaan, yaitu bilangan irasional.
Dimulailah pencarian tentang bilangan tersebut. Dalah satunya adalah dengan
cara berikut. Dimulai dengan segitiga siku-siku sama kaki dengan kaki panjang
1, kita dapat membangun segitiga siku-siku di sampingnya yang hypotenuses
panjangnya adalah  dan seterusnya. Konstruksi ini
sering disebut sebagai Square Root Spiral.
dan seterusnya. Konstruksi ini
sering disebut sebagai Square Root Spiral.
Sejarah dari Teorema Pythagoras dapat
dibagi sebagai berikut:
1.
Pengetahuan dari Triple
Pythagoras,
2.
Hubungan antara sisi-sisi dari
segitiga siku-siku dan sudut-sudut yang berdekatan,
3.
Bukti dari teorema.
Sekitar 4000 tahun yang lalu, orang Babilonia dan orang Cina telah
menyadari fakta bahwa sebuah segitiga dengan panjang sisi 3, 4, dan 5 harus
merupakan segitiga siku-siku. Mereka menggunakan konsep ini untuk membangun
sudut siku-siku dan merancang segitiga siku-siku dengan membagi panjang tali ke
dalam 12 bagian yang sama, seperti sisi pertama pada segitiga adalah 3, sisi
kedua adalah 4, dan sisi ketiga adalah 5 satuan panjang.
Sekitar 2500 tahun SM, Monumen Megalithic di Mesir dan Eropa Utara terdapat susunan segitiga siku-siku dengan panjang sisi yang bulat. Bartel Leendert van der Waerden meng-hipotesis-kan bahwa Tripel Pythagoras diidentifikasi secara aljabar. Selama pemerintahan Hammurabi the Great (1790 - 1750 SM), tablet Plimpton Mesopotamian 32 terdiri dari banyak tulisan yang terkait dengan Tripel Pythagoras. Di India (Abad ke-8 sampai ke-2 sebelum masehi), terdapat Baudhayana Sulba Sutra yang terdiri dari daftar TripelPythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki.
Sekitar 2500 tahun SM, Monumen Megalithic di Mesir dan Eropa Utara terdapat susunan segitiga siku-siku dengan panjang sisi yang bulat. Bartel Leendert van der Waerden meng-hipotesis-kan bahwa Tripel Pythagoras diidentifikasi secara aljabar. Selama pemerintahan Hammurabi the Great (1790 - 1750 SM), tablet Plimpton Mesopotamian 32 terdiri dari banyak tulisan yang terkait dengan Tripel Pythagoras. Di India (Abad ke-8 sampai ke-2 sebelum masehi), terdapat Baudhayana Sulba Sutra yang terdiri dari daftar TripelPythagoras yaitu pernyataan dari dalil dan bukti geometris dari teorema untuk segitiga siku-siku sama kaki.
Pythagoras
(569-475 SM) menggunakan metode aljabar untuk membangun Tripel Pythagoras.
Menurut Sir Thomas L. Heath, tidak ada penentuan sebab dari
teorema ini selama hampir lima abad setelah Pythagoras menuliskan teorema ini.
Namun, penulis seperti Plutarch dan Cicero
mengatributkan teorema ke Pythagoras sampai atribusi tersebut diterima dan
dikenal secara luas. Pada 400 SM, Plato mendirikan sebuah metode untuk mencari
Tripel Pythagoras yang baik dipadukan dengan aljabar and geometri. Sekitar 300
SM, elemen Euclid (bukti aksiomatis yang tertua) menyajikan teorema tersebut.
Teks Cina Chou Pei Suan Ching yang ditulis antara 500 SM
sampai 200 sesudah masehi memiliki bukti visual dari Teorema Pythagoras atau
disebut dengan "Gougu Theorem" (sebagaimana
diketahui di Cina) untuk segitiga berukuran 3, 4, dan 5. Selama Dinasti
Han (202 SM - 220 M), Tripel Pythagoras muncul di Sembilan Bab
pada Seni Mathematika seiring dengan sebutan segitiga siku-siku. Rekaman
pertama menggunakan teorema berada di Cina sebagai 'theorem Gougu', dan di
India dinamakan "Bhaskara theorem".
Namun,
hal ini belum dikonfirmasi apakah Pythagoras adalah orang pertama yang
menemukan hubungan antara sisi dari segitiga siku-siku, karena tidak ada teks
yang ditulis olehnya yang ditemukan. Walaupun demikian, nama Pythagoras telah
dipercaya untuk menjadi nama yang sesuai untuk teorema ini.
Pengertian Teorema Phytagoras
Dalam
matematika,
teorema Pythagoras adalah suatu keterkaitan dalam geometri
Euklides antara tiga sisi sebuah segitiga
siku-siku. Teorema ini dinamakan menurut nama filsuf dan matematikawan
Yunani abad
ke-6 SM, Pythagoras. . Pythagoras mendapat kredit karena ialah yang
pertama membuktikan kebenaran universal
dari teorema ini melalui pembuktian matematis
Teorema Pythagoras menyatakan bahwa:
Jumlah luas bujur sangkar
pada kaki sebuah segitiga siku-siku sama dengan luas bujur sangkar di hipotenus.
Sebuah segitiga
siku-siku adalah segitiga
yang mempunyai sebuah sudut
siku-siku; kaki-nya
adalah dua sisi yang membentuk sudut siku-siku tersebut, dan hipotenus
adalah sisi ketiga yang berhadapan dengan sudut siku-siku tersebut. Pada gambar
di bawah ini, a dan b adalah kaki segitiga siku-siku dan c
adalah hipotenus.
Akan halnya, Sulbasutra India juga menyatakan bahwa:
Tali yang direntangkan sepanjang panjang diagonal
sebuah persegi panjang akan menghasilkan luas yang dihasilkan sisi vertikal dan
horisontalnya. Menggunakan aljabar,
kita dapat mengformulasikan ulang teorema tersebut ke dalam pernyataan modern
dengan mengambil catatan bahwa luas sebuah bujur sangkar adalah pangkat dua
dari panjang sisinya:
Jika sebuah segitiga
siku-siku mempunyai kaki dengan panjang a dan b dan hipotenus dengan
panjang c, maka :
Luas daerah hitam pada gambar (1) adalah 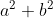
Luas daeraeh hitam pada gambar (2) adalah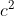
Dengan demikian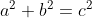
^{2}+&space;4&space;\&space;.\frac{1}{2}&space;a&space;\&space;.&space;\&space;b&space;=&space;c^{2})


3 Bukti dari Euclides
Ada
banyak bukti yang menunjukkan kebenaran teorema pythagoras. Beberapa
diantaranya adalah bukti pythagoras yang dikemukakan oleh Pythagoras, Bhaskara,
Garfield, dan Euclid.
Berikut
ini beberapa pembuktian dari teorema pythagoras :
1 Bukti dari Sekolah Phytagoras
Luas daeraeh hitam pada gambar (2) adalah
Dengan demikian
2 Bukti dari
Bhaskara
Bukti berikut ini pertama kali terdapat pada karya
Bhaskara (matematikawan India sekitar abad X). Bangun ABCD di bawah ini berupa
bujur sangkar dengan panjang sisi c. Di dalamnya dibuat empat buah
segitiga siku-siku dengan panjang sisi a dan b.
Luas PQRS + 4
x Luas ABQ = Luas ABCD
3 Bukti dari Euclides
Bukti berikut ini pertama kali diberikan oleh
Euclides. Perhatikan gambar di bawah ini.
DBQE =
NLBD ……kedua bangun kongruen
=
MLBC …...alas sama BL dengan tinggi tetap BD
=
SRBC …....alas sama BC dengan tinggi tetap BR








keren banget kak
ReplyDeleteElever Media Indonesia